Linear programming is a topic we have widely explained so far!
Linear programming is still used today, and if you want to find out what linear programming is, click here!
Also, check articles for calculating slack and corner points!
In this article, we will focus on dual and shadow prices in linear programming, so keep reading if you want to find out about those terms!
Advertising links are marked with *. We receive a small commission on sales, nothing changes for you.
How Do You Find Dual Price in Linear Programming?

First, we need to know what a dual price is.
The dual price is a quantity that is related to each constraint.
Let’s see a quick example below.
The units of the dual price are a dollar per kilogram if the units of the objective function are dollars and the units of the relevant constraint are kilograms.
The rate at which the objective function value will grow as the right-hand side or constant term of a constraint is slightly increased is known as the dual price of the constraint.
So, to conclude…
The dual price indicates the cost of achieving the last unit of the minimum production goal in the event of a greater-than-or-equal restriction, such as a minimum production level constraint.
To answer the question “Where can you find dual price in linear programming?” keep reading!
The goal function’s units are divided by the constraint’s units to determine the units of the dual pricing.
Also, an “=” constraint’s dual price may be positive or negative.
A fantastic fact is that demand-based dual pricing is conceivable! Look at the example below to understand the conceivable part.
For instance, an airline may charge one price for early bookings and a higher price for last-minute reservations.
Additionally, firms that depend on tourism in many underdeveloped countries use dual pricing techniques.
What is also interesting about dual prices?
The dual prices are some of the most intriguing values in the solution to a linear program.
Each limitation is provided with a dual price.
Only when a constraint is binding does the dual price become positive.
And, if the constraint is loosened by one unit, the dual price indicates the improvement in the objective function.
What is Dual Value in Linear Programming?
According to the principle of duality in linear programming, every linear programming issue has a related linear programming problem that may be derived from it.
The primary linear issue is “Primal,” while the derived linear problem is “Dual.”
The initial linear programming issue must first be expressed in its standard form before the duality can be solved.
In standard form, the variables in the problem must all be non-negative, and the minimization and maximization cases are denoted, respectively, by the ” ≥ ” and ” ≤ ” signs.
Look at the example of the dual value in the next paragraph!
Example of Dual Value in Linear Programming
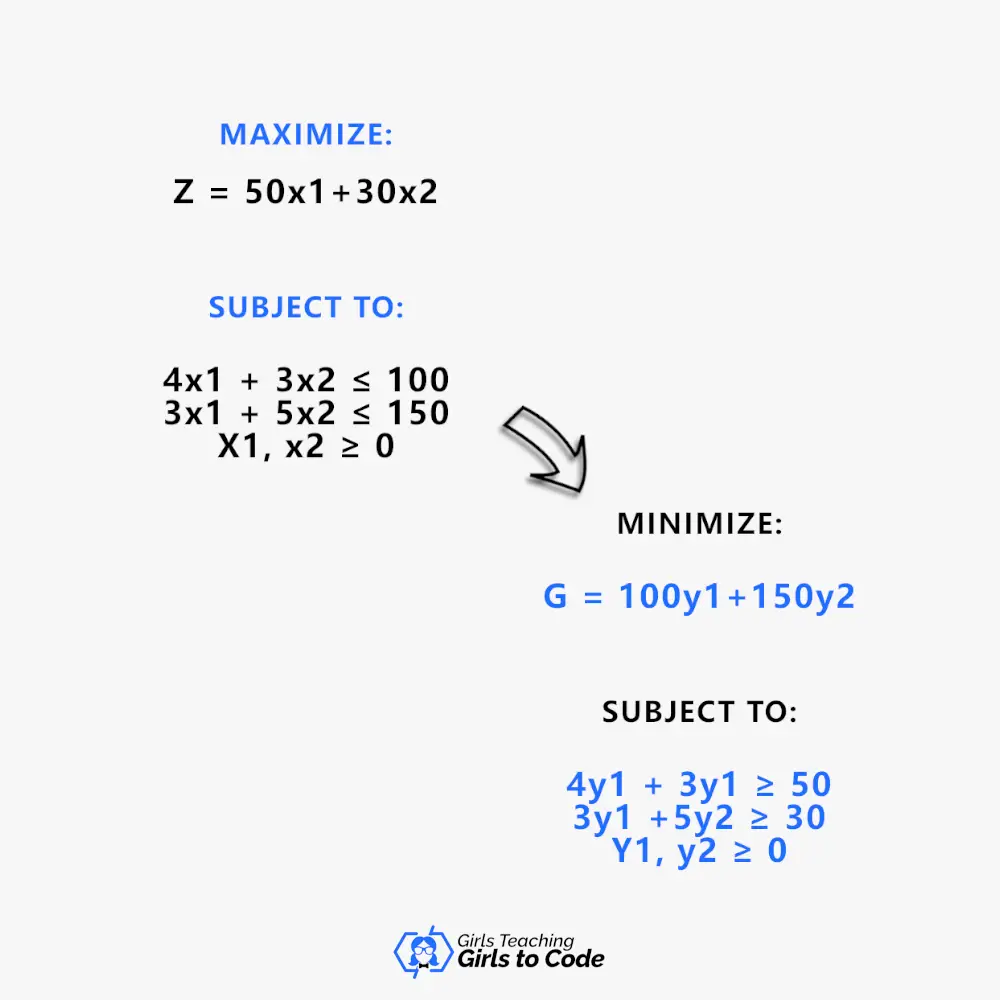
Basically, to the initial linear programming issue mentioned in the picture, the duality may be applied as said in the second mentioned linear programming issue.
While developing the dual linear programming problem, the following observations were made:
The dual problem is of the minimization type, whereas the primary or original linear programming issue is of the maximizing type.
While the coefficient of the variables in the objective function of a primal problem has changed to become the constraint value in the dual problem, what changes for the constraint values?
Basically, the constraint value of 100 became the coefficient of the variable y1.
On the other hand, the constraint value of 150 of the primary problem became the coefficient of the variable y2 in the objective function of a dual problem.
The first row in a dual problem is now the first column in the constraint inequality of a primal problem, and vice versa for the second column in the constraint inequality of a primal problem.
Inequalities’ directions have also shifted, with the dual problem’s sign being the opposite of a primal problem.
As a result, although the inequality sign in the primary problem was “≤,” it now reads “≥” in the dual problem.
How is Shadow Price Calculated in Linear Programming?
As per usual, we need to understand what the shadow price is.
Basically, a shadow price is an estimated cost for a good or service that isn’t typically offered for sale or priced in the market.
In more detail, a shadow price is…
The increase in value (often increased contribution) resulting from having one more unit of a limited resource accessible at its original cost can be used to determine a resource’s shadow price.
Since there is existing slack, non-critical restrictions will have zero shadow pricing.
In economics, the “Shadow price” is a substitute value for an item or service without a market price.
It is what someone must give up to obtain an additional unit.
If the beneficiaries’ preferences are known, the shadow price can help assess the costs or advantages of a project.
The shadow price for each constraint, the amount the objective function will change given one additional unit on the right-hand side (RHS) of the constraint and no other modifications, is calculated using Excel or linear programming.
By deducting the original objective function value from the objective function value with one extra unit of the resource on the RHS, the shadow price value can likewise be calculated.
Is Dual and Shadow Price the Same?
Dual pricing is the practice of charging different prices in several marketplaces for the same or similar goods.
It can be a sign that someone intends to discard something.
We can utilize dual pricing to achieve several objectives, including price discrimination or breaking into a foreign market by giving meager prices to purchasers using the foreign currency.
A production process that is now operating as effectively and productively as feasible is what the shadow price represents.
It calculates the additional value resulting from a one-unit increase in the most critical production resource.
This thus denotes the most significant price the manufacturer may demand that additional resource without suffering total financial loss.
Although the value of this pricing is primarily theoretical and employed in economic calculations and difficulties, a real-world example makes it easier to understand.
People can see a company producing widgets with 50 employees.
The amount of extra widgets that could be generated by hiring one more worker is known as the shadow price.
The number also reveals the maximum salary the company may pay an employee before doing so actually costs the company money.
Advertising links are marked with *. We receive a small commission on sales, nothing changes for you.
