A mathematical method called linear programming chooses how to use resources most effectively.
Managers use the technique to select the most effective use of finite resources, such as cash, time, materials, and equipment.
On the other hand, the optimization of a linear function under a set of linear constraints over integer variables is expressed through integer programming.
We can see how both programming methods are intertwined, so it is only natural to ask yourself where the difference is.
In this article, you will find the main difference between linear and integer programming and where you can use both.
Advertising links are marked with *. We receive a small commission on sales, nothing changes for you.
What Is The Difference Between Linear Programming and Integer Programming?

First, let’s talk a little bit more about linear programming.
The best result of a linear function is chosen through a procedure called linear programming.
Making a few straightforward assumptions is the most exemplary technique for carrying out linear optimization.
The objective function is referred to as the linear function, and the relationships in the real world may be pretty complex.
However, such relationships may be represented using linear programming, making studying them simpler.
Numerous sectors, including industry, energy, telecommunications, and transportation, use linear programming, which shows you how vital linear programming is.
If you want to find out more about linear programming, click here!
Now, let’s find out what integer programming is.
An optimization or feasibility issue in mathematics where some or all variables must be integers is known as an integer programming problem.
The phrase frequently applies to integer linear programming (ILP), where the objective function and constraints (apart from the integer constraints) are linear.
Programming in integers is NP-complete. One of Karp’s 21 NP-complete problems is the specific case of 0-1 integer linear programming, wherein the unknowns are binary, and only the limitations need to be met.
The issue is a mixed-integer programming problem if some decision variables are not discrete.
Numerous industrial productions, including job-shop modeling, use mixed-integer programming.
The best example would be agriculture. Agriculture today uses a lot of mathematical and similar equations that help with planning.
For example, in agriculture, workers need plans for
- working hours,
- capital,
- seeds,
- fertilizers, and much more.
Also, many fields, including engineering, management, communication, and the economy, use integer programming to address optimization issues.
Integer Programming Example
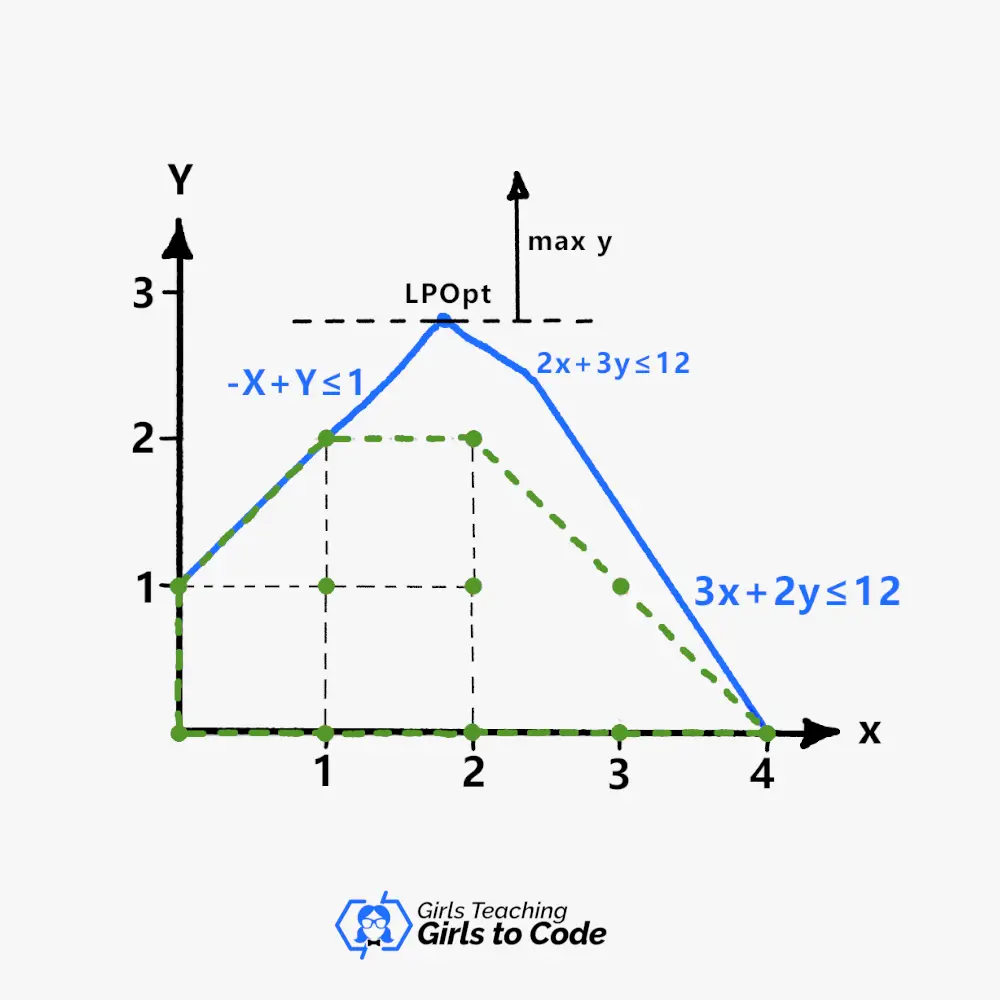
The plot above shows the problem below:
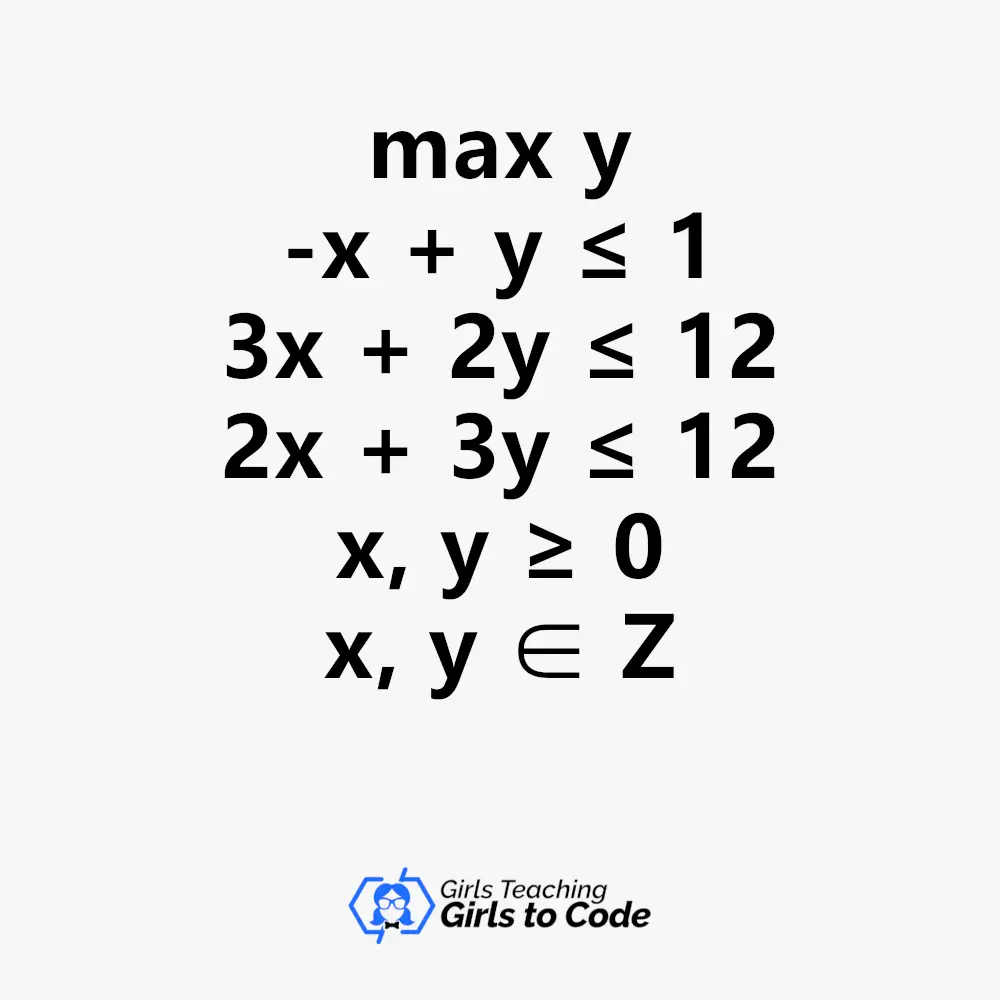
The green dashed lines represent the convex hull of the feasible integer points, the shortest convex polyhedron that encompasses all these points.
The relaxation polyhedron is set through inequalities.
These inequalities are without integral constraints and you can see them on the blue lines in the view above.
The optimization is to raise the black dashed line as much as possible while keeping it in contact with the polyhedron.
The points (1, 2) and (2, 2), which have an objective value of 2, are the best solutions to the integer issue.
What Is The Difference Between Linear Programming And Nonlinear Programming?
Here is the primary difference between linear and nonlinear programming.
Basically, the former assists in identifying the best solution from a set of parameters or requirements with a linear relationship.
On the other hand, the latter assists in identifying the best solution from a set of parameters or requirements with a nonlinear relationship.
Since it aids in identifying the most optimal solution to a given issue, linear programming is crucial in mathematical optimization approaches.
Contrarily, nonlinear programming is a mathematical technique for determining the best course of action while accounting for nonlinear restrictions or the goal function.
Is Dynamic Programming a Type of Linear Programming?
A famous mathematical technique for handling linear and nonlinear optimization issues is dynamic programming (DP).
The name “dynamic” refers to the fact that the approach is typically used to produce a series of optimal choices that are tailored to scenario changes that happen dynamically throughout time.
The method’s basic premise is that the solution to an issue may be found by moving backward from the problem’s conclusion—where only one more option remains—to its inception (where no decision has been made).
In other words, the approach is “recursive” since it divides a big problem’s solution into a series of smaller, more manageable ones.
A dynamic programming formulation does not call on linearity assumptions in contrast to linear programming.
The approach may therefore be used to solve a greater variety of issues. This adaptability is undoubtedly very appreciated.
The representation of an optimization issue as a dynamic program is extremely problem specific; thus, it is not without a cost.
Nevertheless, formulations for dynamic programming are frequently regarded as works of art because of this.
Advertising links are marked with *. We receive a small commission on sales, nothing changes for you.
