How To Find Corner Points in Linear Programming?

Corner points are one of the most critical things in linear programming you can find on graphs. 

There are so many instructions on finding a corner point, but all of it is confusing and sometimes hard to understand. 

In this article, you will find out how to locate the corner point, what it is, and how to solve linear programming problems using the corner points. 

What Are Corner Points in Linear Programming Problem?

First, let’s define a linear programming problem, or short, LPP. 

Linear Programming Problems (LPP) aims to determine the best value for a given linear function. 

The ideal value may be either the highest or lowest value. 

The specified linear function is regarded as an objective function in this situation.

A linear program is a restricted optimization model that satisfies the following criteria;

1. Criteria say that the decision variables must be continuous within a predetermined range.
2. Criteria say that the left-hand side of the restrictions (inequalities) and the goal function must be linear.

Also, three key components make up a restricted optimization model in LPP:

1. The variables of a system or problem that we must optimize are called decision variables. They are represented by algebraic symbols like x, y, etc.
2. The objective function is the evaluation criterion that we must increase or decrease (maximize or minimize). We must maximize or minimize a function of the choice factors; maybe a measure of revenue, the processing time, etc.
3. Any restrictions brought on by science, physics, economics, and other factors are represented as constraints, which are a system of equality and inequality. 

A limitation can significantly reduce the costs spent on each procedure, the weight that can fit in each bag, etc. 

The problem’s ideal solution must meet every restriction.

If you want to find out more about linear programming, click here!

You must be wondering by now where are corner points in this story. 

Keep reading if you want to find out!

Okay, now that we defined the linear programming problem, we can move on to the corner points. 

In LPP, the intersection points of two (or more) constraints define the corner points (or extreme points) of a viable (feasible) area. 

A feasible area must have at least one corner point, whether it is limited or unbounded.

To fully understand this, you have to understand what is a feasible area. 

A feasible set is a collection of points that satisfies an LPP’s restrictions. 

The feasible set is located where all these inequalities cross when the restrictions are plotted on a graph. This area is referred to as a viable area.

Now you have all the information. Keep reading for more!

How Do You Find Corner Points?

There are two ways of finding corner points in a linear programming problem (LPP). 

The two ways are 

1. Algebraically 
2. Graphically 

We will go through both methods. 

Finding Corner Points Algebraically

Take a look at the problem first.

The first step would be to make the restrictions’ disparities into equalities. We will get the system of linear equations shown below:

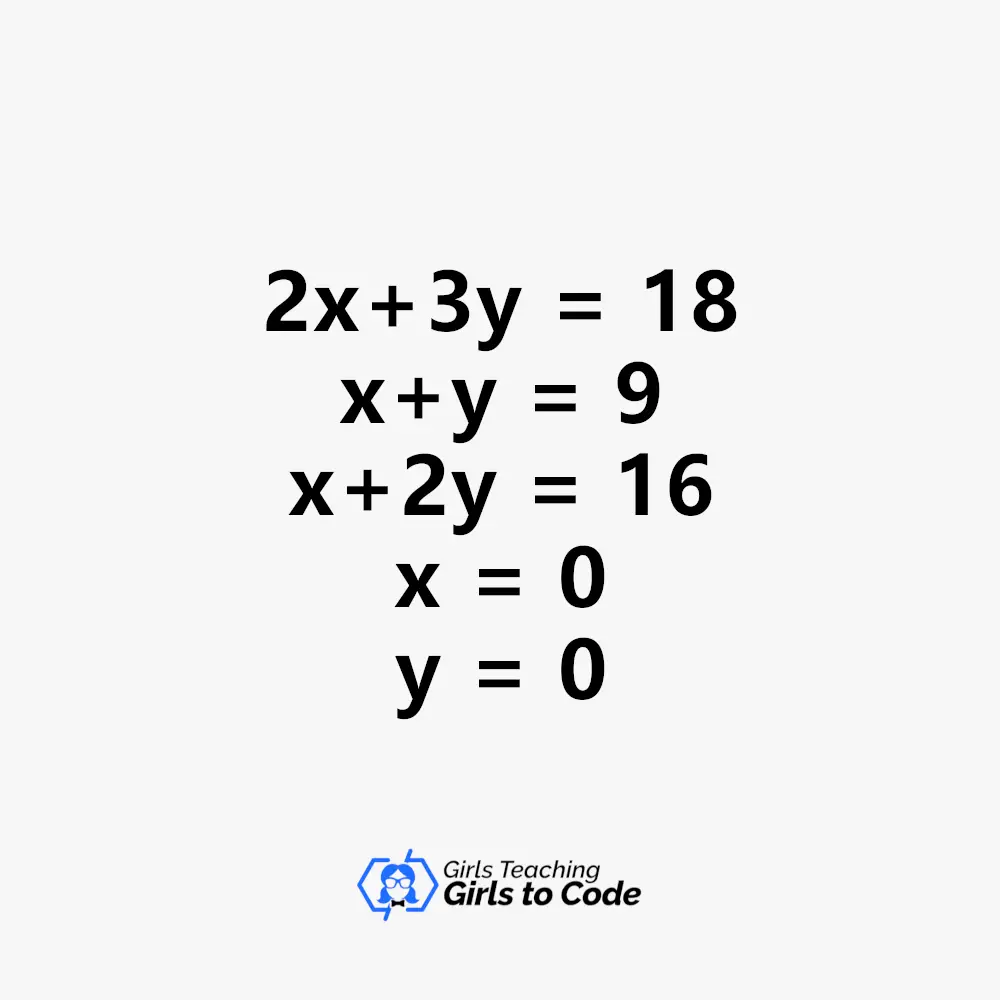
Find the intersection point that meets both equations by solving these linear equations using a pair of any two equations at once. Let’s use the first two equations to demonstrate this:

As a result, the equations 2x+3y=18 and x+y=9 have a solution at the position (9, 0).

Similarly, locate the intersection sites for each additional set of equations’ solutions.

Keep reading for the third step.

To this collection of crossing points, apply the inequality restrictions, and then take out the ones that fulfill each inequality. 

These are our cornerstone points. 

Any point outside of the feasible zone does not satisfy every inequality restriction.

So, the corner point is at (9, 0). However, the point (12, 14) is beyond the feasible zone since it violates the x 0 conditions.

Finding Corner Points Graphically

Let’s stick with the LPP issue that was first discussed in part prior. Follow these methods to determine the viable region’s corner points graphically:

Make the restrictions’ disparities into equalities. The following line equations will be obtained:

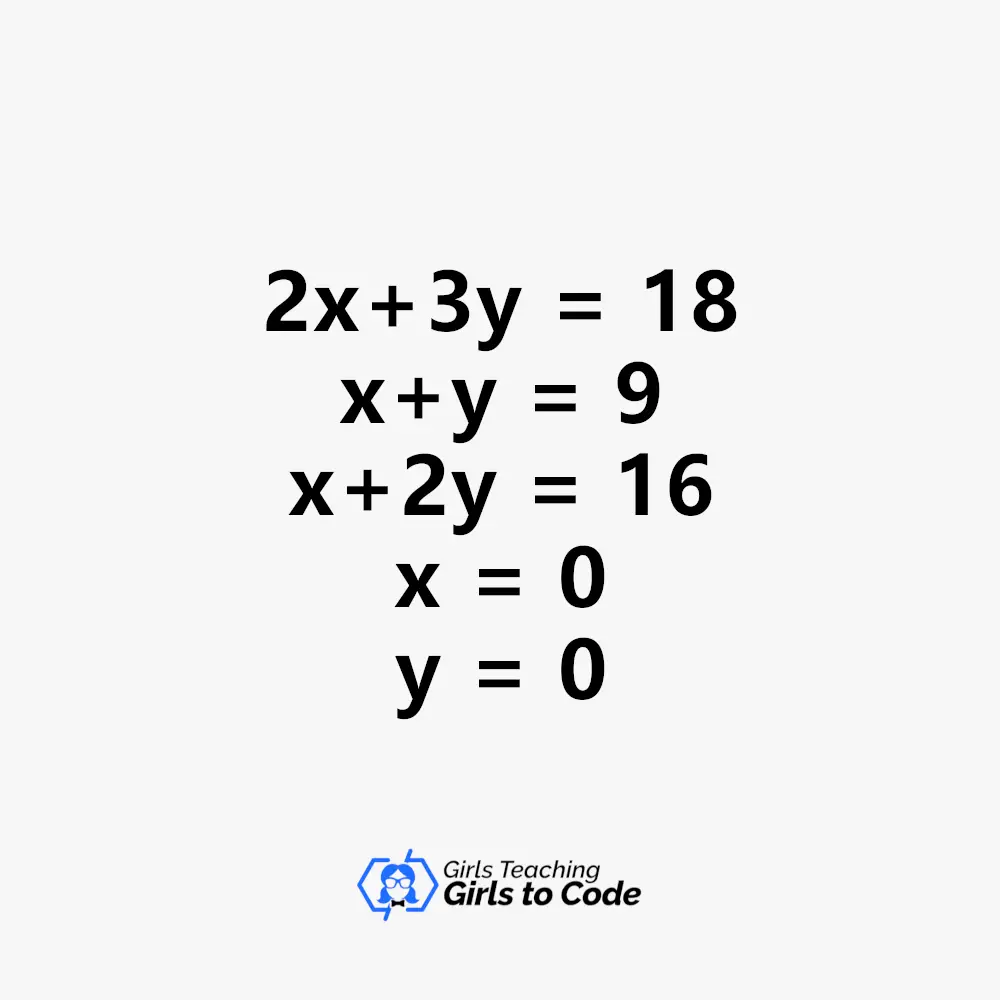
Draw a graph showing these lines. The x- and y-intercepts may be found using a simple procedure. 

Substituting y=0 gives us x=9, the x-intercept for the line 2x+3y=18. As a result, the x-intercept is (9, 0). 

Similarly, use x=0 as a replacement to get the y-intercept (0,6).

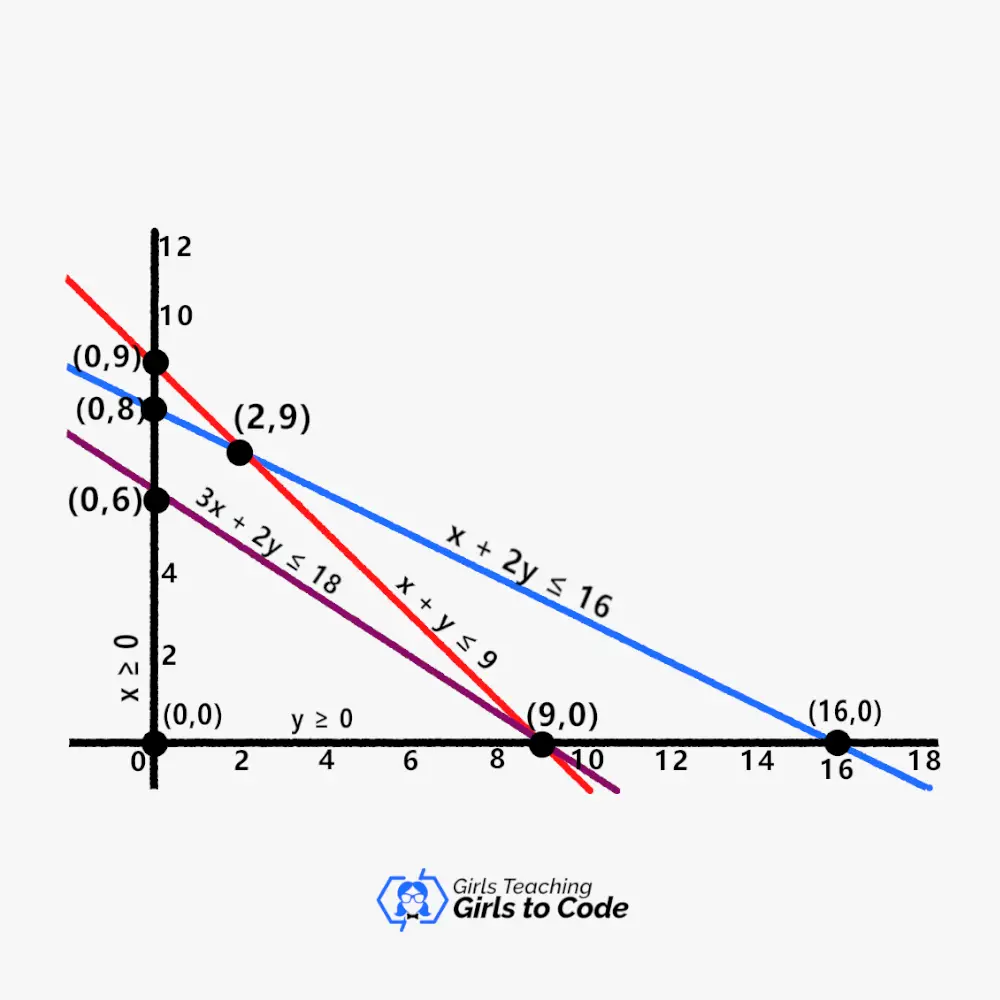
The portion of the graph that satisfies each constraint is shaded. It is the LPP’s practicable area. It is the point at which all of the constraints’ inequalities cross.

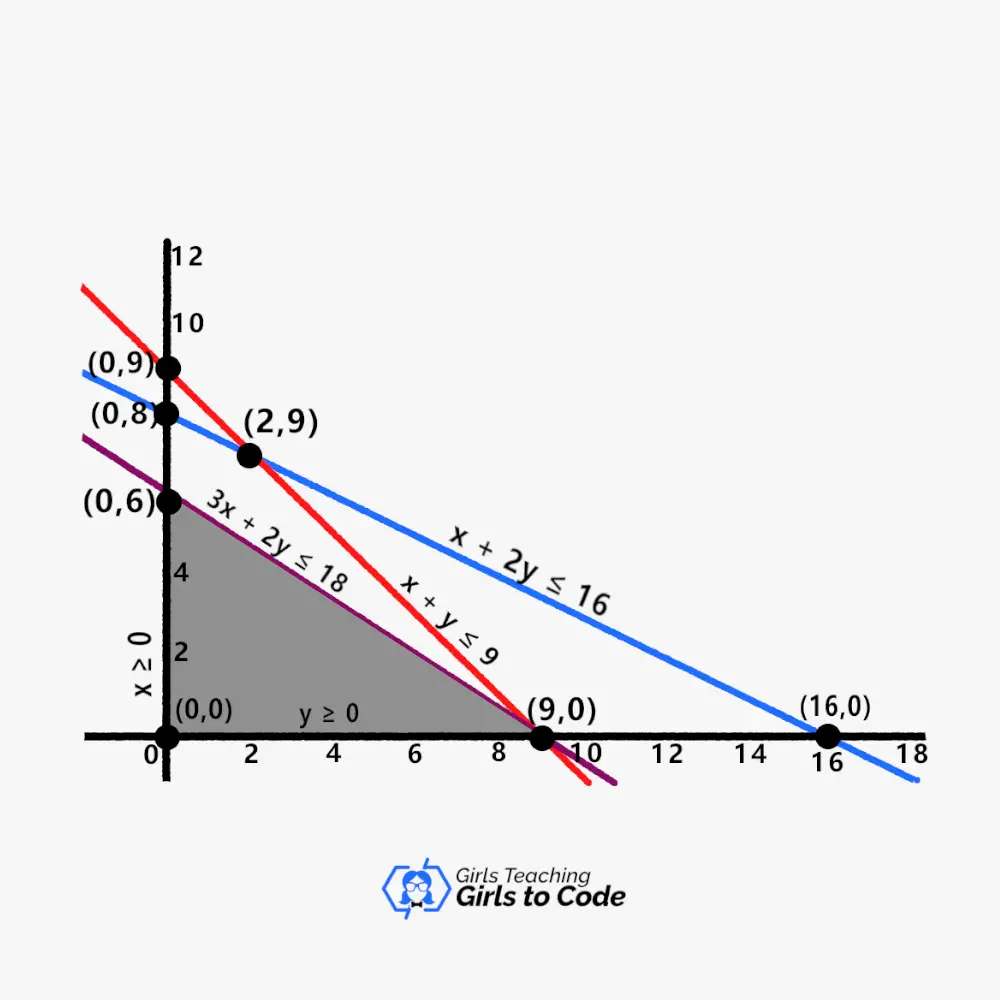
Draw the corner points of the viable region’s border from its vertices. This way, derived corner points are (9,0), (0,6), and (0,0)

How Do You Identify a Corner Point in Linear Programming?

The vertex of the feasible area is the actual corner point. 

When you have the graph of the linear inequality system, you can quickly identify the corner points by looking at the graph.

Some of the coordinates of the center points may need the solution of a system of linear equations.

For instance, the location where the lines x + 2y = 16 and x + y = 9 cross provides the answer (2,7).

You can locate this point quickly through many methods, such as: 

1. Substitution, 
2. graphing, 
3. elimination, 
4. matrix inverses,
5. Cramer’s rule, etc. 

The corner points for this system are (0,0), (0,8), (2,7), (6,3), and (8,0).

It is important to note that while every intersection of two lines results in a corner point, not every such junction does.

For instance, the intersection of 3x + 2y = 24 and x + y = 9 at the position (6,3) is not a corner point since it is beyond the feasible zone. 

However, the intersection of 3x + 2y = 24 and x + 2y = 16 is the corner point. 

How Do You Solve a Linear Programming Problem With the Help of Corner Points?

A linear programming issue will have at least one of the corner points as the best solution. 

Follow these methods to determine the corner points’ best, optimal solution:

1. At each corner, evaluate the goal function.
2. Find the corner point that produces the objective function’s most significant value if the objective is to maximize it.
3. Find the corner point that produces the objective function’s smallest value if the objective is to minimize it.

Keep in mind that numerous corner spots may offer the best option.

Let’s assess the goal function in our illustration to identify the best course of action:

The corner point is P = 30x + 40y 

(9,0)	270	Maximum
(0,6)	240
(0,0)	0

Our goal was to maximize P=30x+40y; therefore, the corner point is where the ideal solution, 270, occurs (9,0).

So this is an example of how to solve a linear programming problem using corner points.

With corner points, it is possible to find the optimal solution to the linear programming problem. 

That’s it! Hopefully, you understand the corner points now!