Can A Function Have Repeating X Values?

Whether you are learning how to code, or just trying to pass your math exams, having a thorough understanding of functions is necessary.

In fact, a function is arguably the most important concept that you will come across in your studies.

However, we know that functions can be tricky to get to grips with. Learning how to interpret them is akin to learning a new language!

It will take time, patience, practice, and a good teacher – that’s where we come in!

When students begin to learn about functions, some of the most common questions are about whether a function can have repeating x values or y values, and if not – why?

If you’ve found yourself pondering such a question, take a look at our in-depth guide below.

We cover everything you need to know, from the definition of a function to what happens when there are infinitely many solutions and everything in between!

Check it out – you’ll be a master of functions in no time!

What Is A Function?

Before we get into the details, it’s important to make sure that everyone here is on the same page.

As such, we’re going to take a moment to go back to the basics! First, let’s discuss what a function actually is.

To define functions, we need to use the concepts of independent variables and dependent variables.

To do so, let’s take a look at a simple example.

Consider a graph that measures how much you are paid depending on the number of hours you have worked.

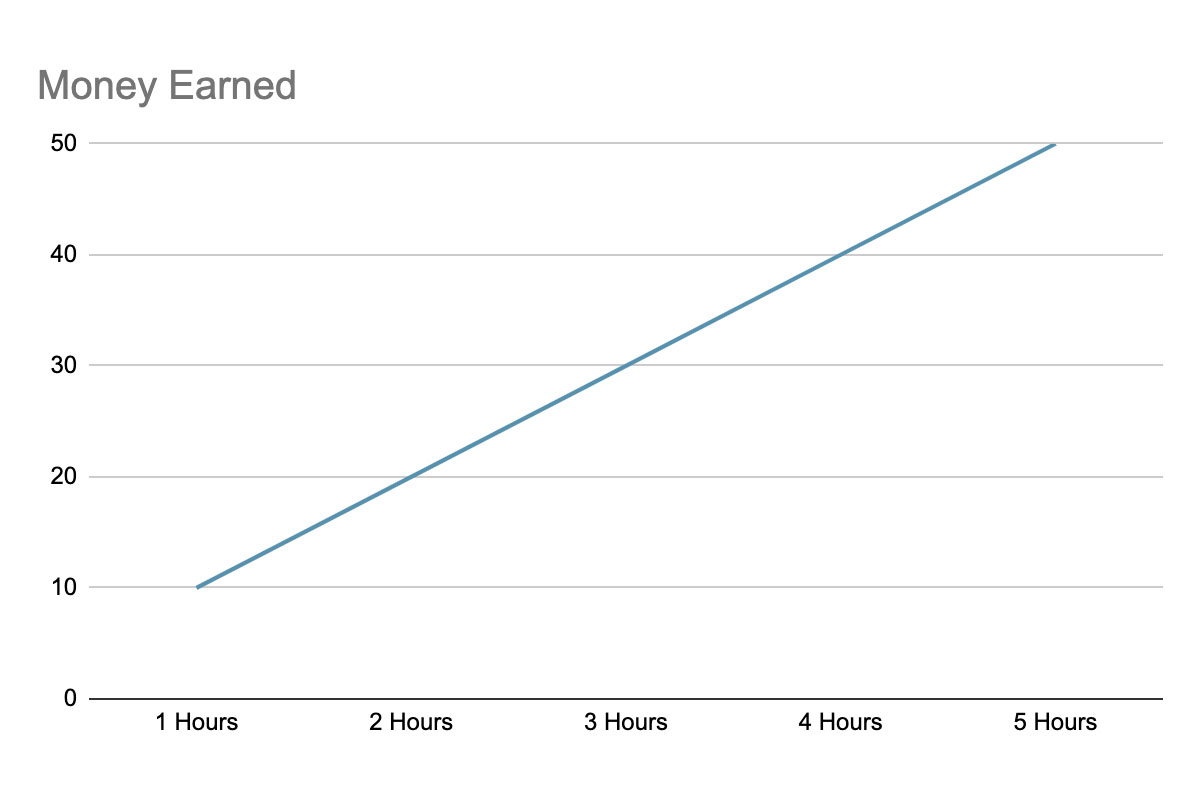
In the graph above, the number of hours worked (along the x-axis) is considered to be the independent variable.

This is because the number of hours that you work affects the amount of money that you earn.

The money earned (along the y-axis), is considered to be the dependent variable.

This is because the amount of money you earn is completely dependent on the number of hours that you work.

Generally speaking, the dependent variable is always represented as y, and the independent variable is always represented as x.

As such, in this case, money earned can be denoted as y, and the hours worked can be denoted as x.

Now, we can define a function as a special kind of relation between the x and y variables.

Functions assign one value of the dependent variables to each value of the independent variable.

As such, in a function, there can only ever be one x-value for each y-value.

Can A Function Have Repeating X Values?

So, by definition of a function, a function absolutely cannot have repeating x-values.

If a function were to have repeating x-values, this would contradict the definition of a function, and so the function in question wouldn’t be a real function.

Can A Function Have Repeating Y Values?

However, that isn’t to say that a function can’t have repeating y-values. In fact, it is common for a function to have repeating y-values.

This instance happens when two x-values lead to the same y-value.

Although, if a function has a repeating y-value, it cannot be described as a one-to-one function.

A one-to-one function is a function wherein there are no repeated y-values. For every x-value, there is just one y-value.

You can tell when a function is one-to-one by looking at the graph.

If you draw a horizontal line across the graph, and it cuts the graph line more than once, it is not a one-to-one function.

As you can see, the graph above is a one-to-one function.

How Many Times Can A Y-Value Repeat?

There is no limit as to how many times a y-value can be repeated. Seriously!

It is actually possible for a y-value to be repeated an infinite number of times many times.

This means that the equation for the function will have infinitely many solutions.

This can sound a bit confusing. So, let’s take a look at some clear examples of such functions below.

You’ll notice that none of them are one-to-one, because they all fail the horizontal line test described above.

Y-Value Repeated Twice

Consider the function y=x2. The graph is below.

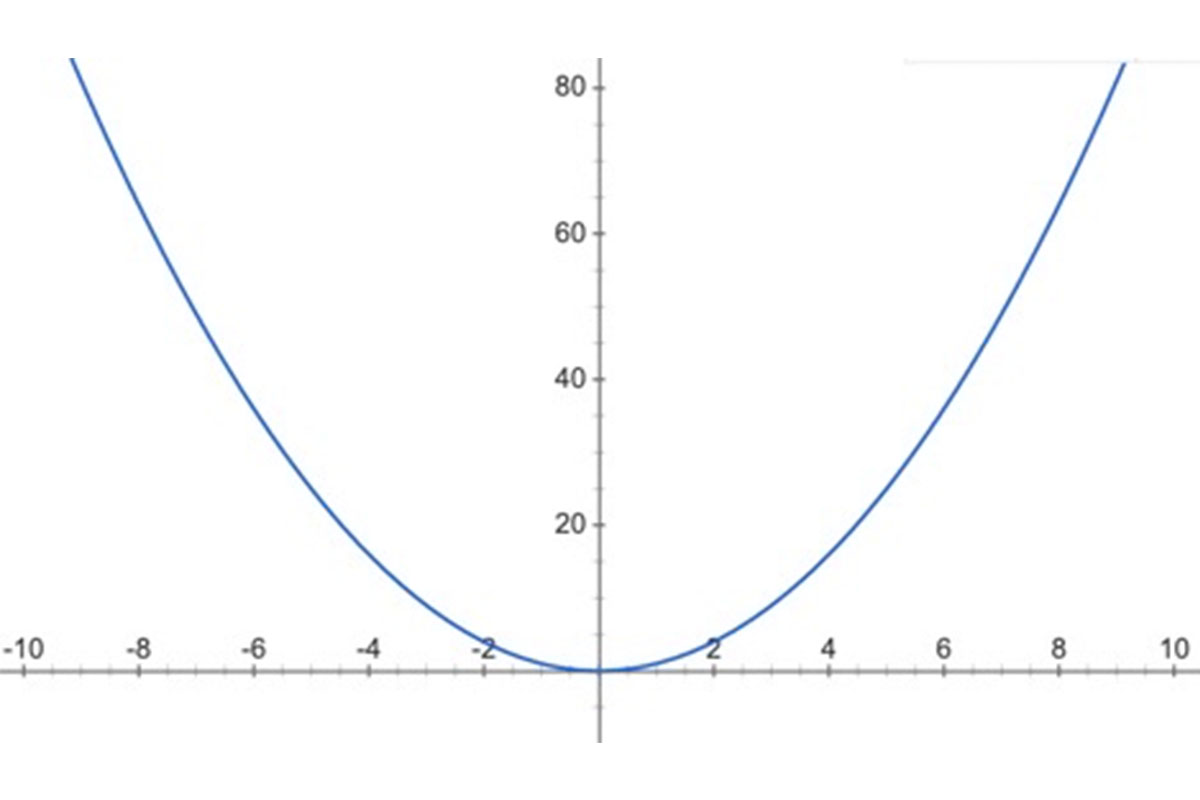
We can see that for every y-value, there are two x-values. For instance, we can consider the value y = 16.

We get this y-value when we substitute x = 4 and x = -4 into the equation y=x2.

Y-Value Repeated Three Times

Now, let’s take a look at a function that has a y-value that is repeated 3 times. Consider the function f(x) = 2×3+3×2-11x-6 .

This is a cubic function. If we factorize it, we will get f(x) = (x-2)(2x+1)(x+3). This means that, when y = 0, we get three x-values.

The three x-values are 2, -½, and -3. We could describe these solutions as coordinates to illustrate the repetition of y-values as such: (2, 0), (-½, 0), and (-3, 0).

Y-Value Repeated Four Times

Let’s keep going! Consider the following function: f(x) = 2×4-3×2 . The graph for this function is featured below.

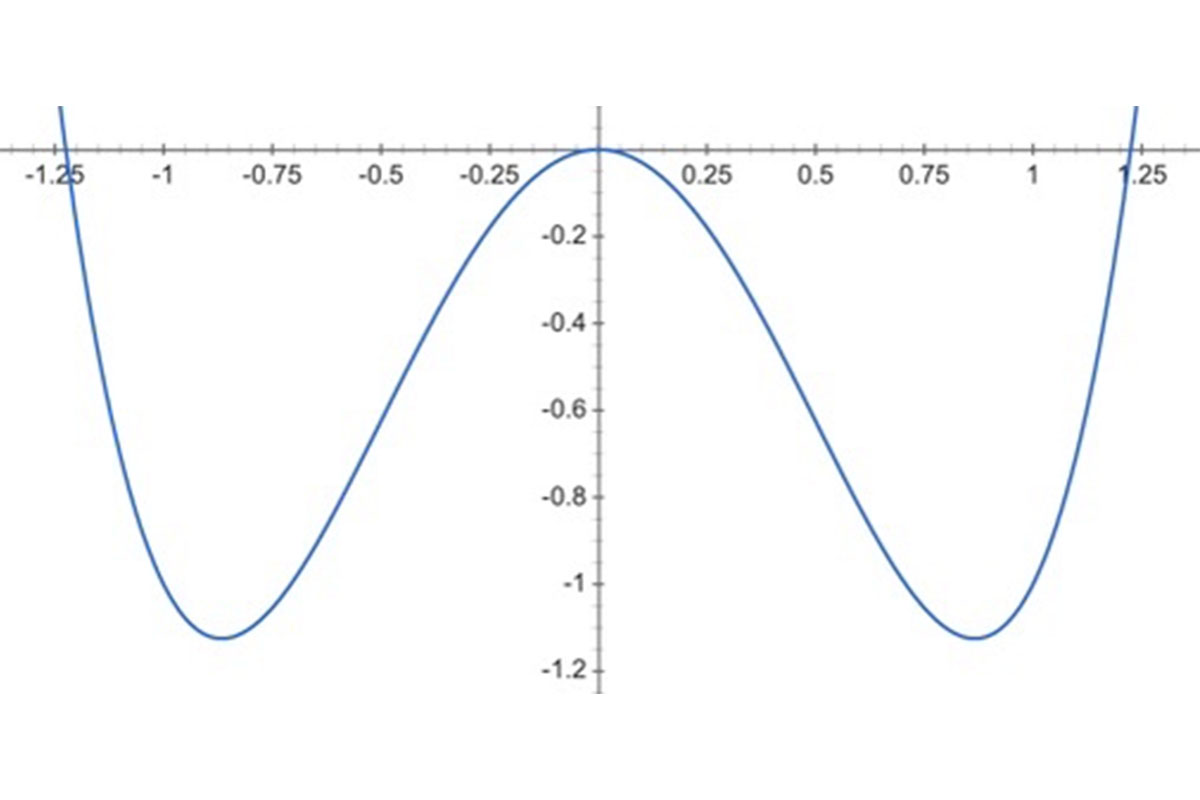
As you can see from the graph, there are four different x-values for each y-value.

To prove this, you can draw a horizontal line through any point of the graph.

For example, if you draw a line through y = -1, it crosses the graph four different times. Take a look below.

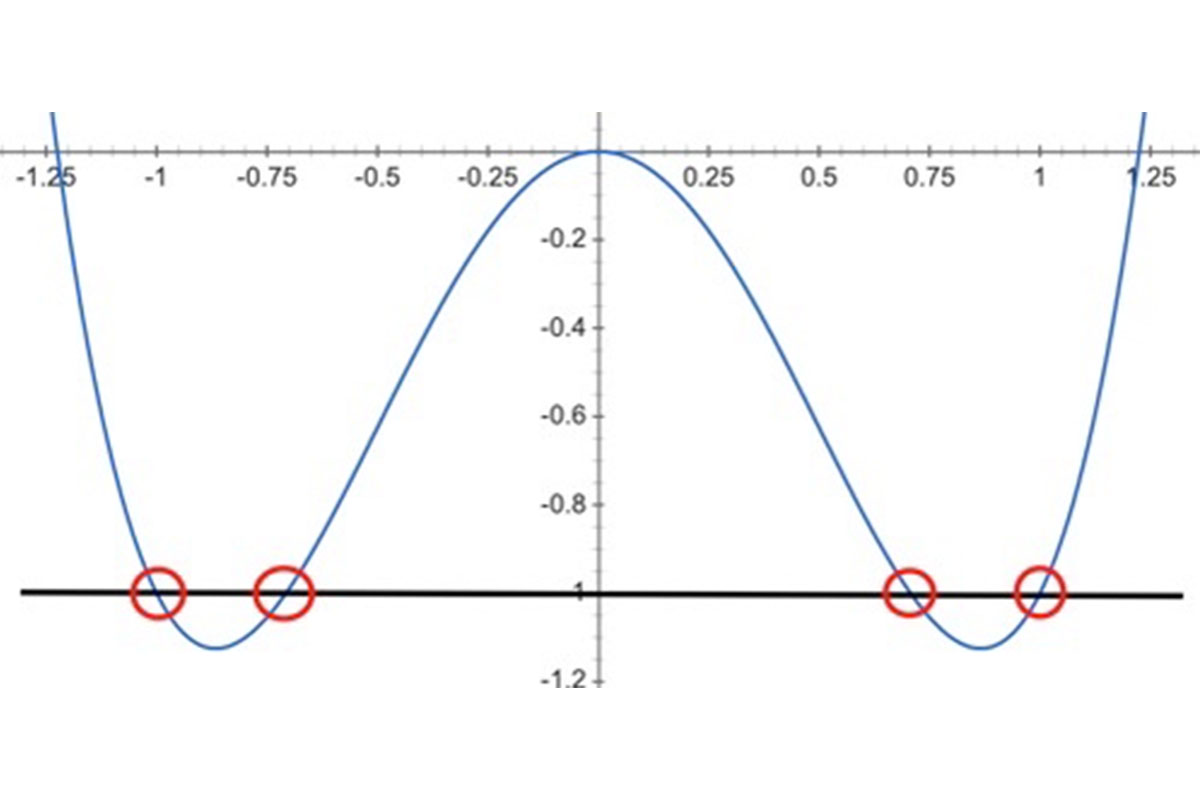
The x-values of the points that have been circled each provide an output (or y-value) of 1. This type of function is called a quartic function.

You can also use an algebraic method to see the repeated values.

Y-Value Repeated Infinitely Many Times

Now, let’s take a look at a function with infinitely many y-values. It is likely far more simple than you think it is!

Consider the function f(x) = 5. This function is linear, and can be represented on a graph by a horizontal line.

Take a look at the graph below.

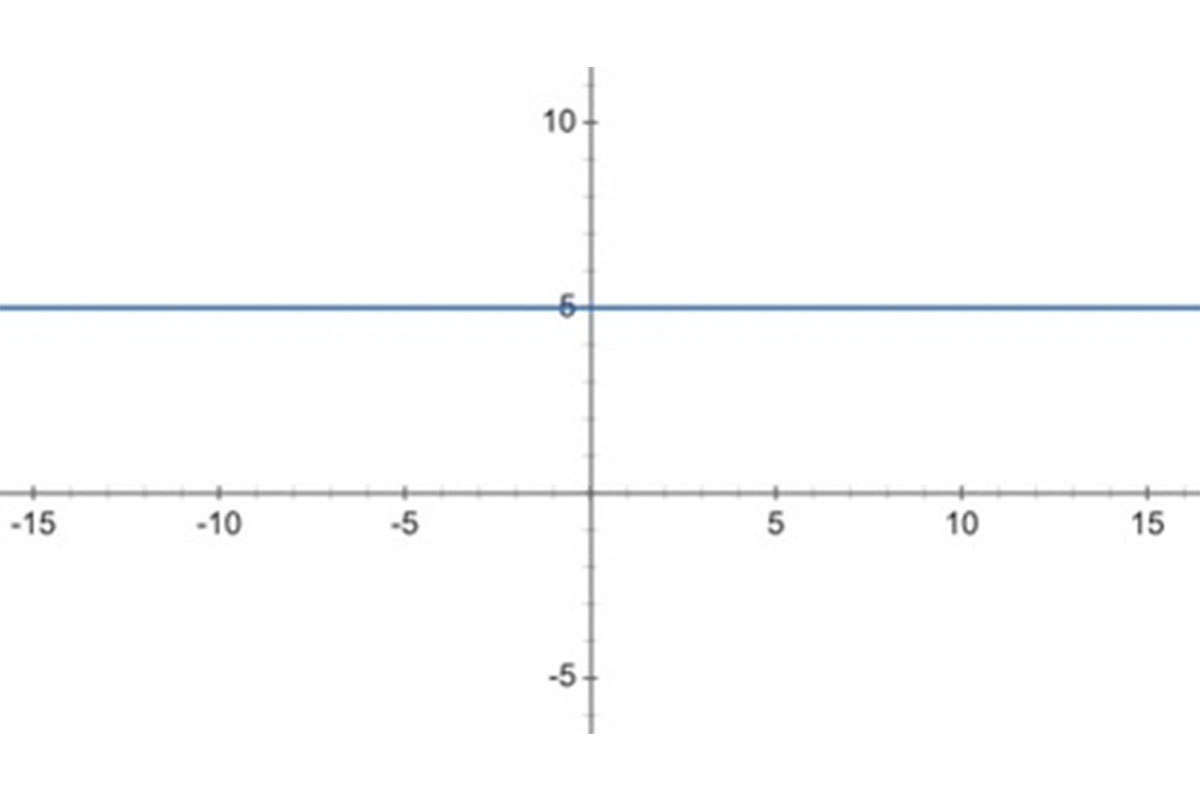
As you can see, regardless of what x value you choose, the y-value will always be the same. For example, f(10) = 5 and f(-15) = 5.

As such, the value y = 5 is repeated infinitely many times.

Conclusion

Functions are a very important part of coding, programming, and mathematics in general.

As such, it is important that you understand them thoroughly.

We hope that this article has helped you to understand why a function cannot have repeating x-values so that you can move on to bigger and better concepts!